서론
Page rank에서 rank란 중요도를 의미한다.
따라서 page rank라 하면 page의 중요도를 말한다.
Page의 중요도를 계산하는 기본 아이디어는 page끼리 걸린 링크를 이용하자는 것이다.
예를들어 M이라는 사람이 포스팅한 자바 관련 page가 상당히 유명하다고 하자.
이때 자바를 공부해서 포스팅하는 여러 사람들이 위 page를 참고했다는 의미로 링크를 걸어놨다.
그럼 M의 특정 페이지의 중요도가 올라가게된다.
페이지와 링크라는 개념을 사용하기 보단, 조금 더 추상화 하여 그래프 형태로 문제를 다시 구성할 수 있다.
이제 어떻게 계산할지에 대해 알아보자.
Random Walks
Random walks는 사람들이 페이지를 돌아다니는 모습을 추상화했다고 할 수 있다.
웹에 보이는 page가 10개가 있다고 해보자.
1. 맨 처음에는 10개중에 하나를 랜덤으로 선택한다.
2. 1번에서 고른 page에 존재하는 링크들 중 하나를 20% 확률로 방문한다.
3. 2번에서 링크를 방문하지 않았다면, 다시 10개중에 하나를 랜덤으로 선택한다.
Page rank는 위와같은 random walk를 무한번 반복했을때, 각 페이지에 방문할 확률이라고 할 수 있다.
따라서 page rank 문제는 총 3가지가 주어져야한다.
1. Page들
2. Page 끼리의 링크 여부
3. 특정 링크를 방문할 확률
이때 page의 경우 그래프의 node, 링크는 edge로 나타낼 수 있다.
문제를 풀어보면서 이해해보고 싶다면, 아래 예시를 보자.
예시 1

위와같이 page와 링크가 주어졌고, 특정 링크를 방문할 확률이 80%라고 하자.
맨 처음에 v1에서 시작한다고 하면, 두번째에 v3를 방문할 확률은 어떻게 될까?
v1은 v3와 v5를 링크로 걸고있다.
따라서 v1에 걸린 링크를 클릭하는 경우라면
1. 80% 확률로 v1에 걸려있는 특정 링크를 방문
2. 그 특정 링크가 v3일 확률이다.
따라서 1번과 2번의 곱이 v1에 걸린 링크를 클릭해서 v3로 갈 확률이 된다.
만약 v1에 걸린 링크를 클릭하지 않는 경우라면
1. 20% 확률로 v1에 걸려있는 특정 링크를 방문하지 않음
2. 5개의 page중 랜덤으로 v3를 고를 확률
따라서 1번과 2번의 곱이 v1에 걸린 링크를 클릭하지 않고 v3로 갈 확률이 된다.
결론적으로 (v1에 걸린 링크를 클릭하는 경우의 확률 + v1에 걸린 링크를 클릭하지 않는 경우의 확률)이 두번째에 v3를 방문할 확률이 된다.
이제 계산해보도록 하자.
v1에는 두개의 링크가 있었다.(v3, v5)
따라서 v3를 50% 확률로 클릭한다는 것을 알 수 있다.
80% 확률로 특정 링크를 방문하는데, v3를 50% 확률로 클릭하므로

v1에 걸린 링크를 클릭하는 경우의 확률은 2/5이다.
v1에 걸린 링크를 클릭하지 않는 경우의 확률은 20% 확률로 v1의 링크 방문 안하면서 5개의 page중 v3를 방문할 확률이므로
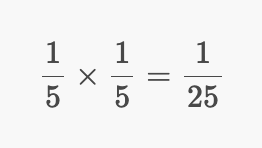
1/25가 된다.
최종적으로 위에서 구한 두 확률을 더하면

11/25 이다.
지금까지 했던 것들을 정리하면, 아래와 같다.
첫번째로 v1을 방문했는데, 두번째로 v3를 방문할 확률은 11/25이다.
예시 2

예시 1의 그래프와 페이지 방문 확률(80%)을 그대로 사용한다고 할때,
첫번째로 v1을 방문했을때, 세번째로 v4에 방문할 확률을 구해보자.
v4는 v3에서 링크를 걸고있고, 그 외 페이지에서 v4를 방문하려면 랜덤으로 방문하는 경우밖에 없다.
즉, 크게 두가지 경우로 나뉠 수 있다.
1. 두번째에 v3에 방문했고, v3의 링크를 타고 v4를 방문하는 경우
2. 두번째에 v3에 방문하지 않았고, 랜덤으로 v4를 방문하는 경우
1번부터 차근차근 확률을 구해보자.
우린 첫번째 예시를 풀어보면서 두번째에 v3에 방문할 확률이 11/25임을 알아냈다.
같은 방식으로 두번째 v3에 방문한 경우에서 두가지 경우가 생긴다.
1-1. v3의 링크들중 하나를 80%로 골라서 방문하는데, 그게 v4
1-2. v3의 링크들을 고르지 않고 랜덤으로 v4를 방문
v3는 링크를 두개 가지고 있다.(v2, v4)
따라서 1-1의 경우 다음과 같이 계산된다.

여기에 두번째에 v3를 방문할 확률이 11/25 였기 때문에 이를 곱해주면 다음과 같다.

1-2의 경우, v3의 링크를 고르지 않을 확률이 20%이고, page가 총 5개이므로 v4를 랜덤으로 방문할 확률이 1/5이므로 다음과 같이 계산된다.
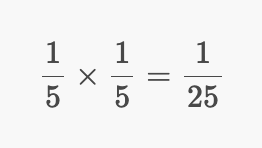
1-1과 마찬가지로 두번째에 v3를 방문할 확률이 11/25을 곱해주면 되는데 잠시 값을 구하지 말고 식의 형태로 남겨놓자.

따라서 두번째에 v3에 방문했고, v3의 링크를 타고 v4를 방문하는 경우는 다음과 같다.
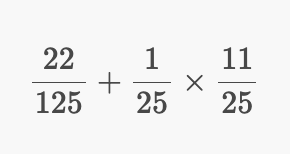
이제 2번에 대한 확률을 구해보자.
두번째에 v3에 방문하지 않았고, 랜덤으로 v4를 방문하는 경우를 구해야한다.
두번째에 v3를 방문할 확률이 11/25였기 때문에 두번째에 v3를 방문하지 않을 확률은 (1 - 11/25)이다.
이는 14/25 라는 것을 알 수 있다.
v3가 아닌 다른 page에서는 v4로 가는 링크가 없기 때문에 랜덤으로 방문하는 경우의 확률만 구하면 된다.
랜덤으로 v4를 방문할 확률은 20% 확률로 링크를 방문하지 않으면서 1/5의 확률로 v4를 랜덤으로 방문하는 경우다.
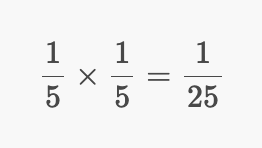
이는 위와 같고, 두번째에 v3에 방문하지 않을 확률은 14/25였기 때문에 이를 곱해줘야한다.
이것도 마찬가지로 수식의 형태로만 남겨놓자.

최종적으로 1번과 2번의 경우를 더해주면 다음과 같다.

근데 두번째 항과 세번째 항은 1/25로 묶을 수 있다.
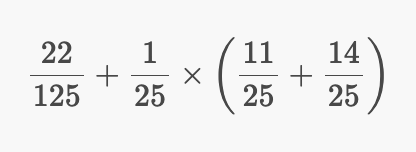
그리고 다음과 같이 정리된다.

이를 통해 알 수 있는 중요한 사실은 다음과 같다.
특정 page p가 t번째에 방문될 확률을 구하려면, 다음 두가지만 알면 된다.
1. p를 링크로 걸고있는 page들이 t-1번째에 방문될 확률
2. 랜덤으로 방문될 확률
예시에서 계산해봐서 알겠지만, 2번의 경우는 특정 페이지를 방문하지 않을 확률과 1 / (전체 페이지 개수)를 곱한 값이 된다.
특정 page p를 가리키는 page들의 집합을 in(p) 라고 정의하고, 특정 페이지 P가 가리키는 page들의 집합을 out(p) 라고 하자.
또한 문제에 주어지는 page들의 집합을 V, 특정 링크를 방문할 확률을 alpha 라고 하자.
이때 t번째에 p를 방문할 확률은 다음과 같이 일반화 할 수 있다.

첫번째 항은 랜덤으로 p를 방문할 확률
두번째 항은 p를 링크로 걸고있는 page들($v \in in(p)$)이 t-1번째에 방문($Prob(v, \ t-1)$)되면서 링크를 타고($\alpha$) p를 방문($\frac{1}{|out(v)|}$)할 확률이다.
한 step 이전의 확률만 알고있으면, 다음 step의 확률을 알 수 있다는 점에서 Markov property 만족하기 때문에 Random walks는 Marokov chains이라고도 불린다.
Power method
위 과정을 반복해서 수행하면 어느 시점에는 각 page를 방문할 확률이 바뀌지 않는다.
Power method는 위 과정을 반복하면 할 수록 실제 page rank 값에 수렴한다는 것을 증명한다.
그러나 이 포스팅에서는 다루지 않는다.
그러나 어떤 식으로 적용되는지 코드로 보이려 한다.

이 예시를 다시 사용해보자.
위 그래프를 인접 리스트 형태로 먼저 만들어준다.
import numpy as np
M = np.array([[0,0,1,0,1],
[1,0,1,0,0],
[0,1,0,1,0],
[1,0,0,0,1],
[0,0,1,0,0]], np.float32)
그리고 M의 각 row에 대해 row별 1의 개수로 나누어준다.
out_count = np.sum(M, axis=-1)[...,np.newaxis]
M = (M / out_count).T
이때 row별 1의 개수는 결국 각 page가 가진 링크의 개수가 된다.
결과를 잘 생각해보면 M의 각 row에 대해 row별 1의 개수로 나누는 것은 위의 일반화 식에서 $\frac{1}{|out(v)|}$ 와 같다.
이때 구해진 M을 stochastic matrix라고 부른다.
이제 모든 page에 대한 $Prob(p, t-1)$ 에 해당하는 벡터를 만들어야한다.
맨 처음에 어느 page에서 시작한다는 말이 없다면, 어느 페이지에서 처음으로 시작할지 모르므로 벡터의 모든 값을 1 / (전체 페이지 개수) 로 만들어야한다.
위에서 풀어냈던 문제는 v1에서 시작했기 때문에 다음과 같이 벡터를 만들어준다.
p = np.array([1,0,0,0,0])
이제 위의 일반화 식에 맞춰서 수식을 구성해야한다.

이는 다음과 같다.
alpha = 4/5
old_p = p
p = (1-alpha)/5 + alpha*(M @ old_p)
위 코드에서 핵심은 M과 old_p의 행렬곱하는 부분(M @ old_p)으로 맨 처음에 M을 만들어줄 때, transpose를 넣어준 이유가 된다.
우리는 p로가는 링크를 가진 page들($v \in in(p)$)에 대해서만 확률을 계산해야했다.
다시 생각해보면, 모든 page에 대해서 계산하는데 p로 가는 링크가 없으면 확률을 0으로 만들면 된다는 것을 알 수 있다.
M과 old_p를 행렬곱 하게되면, M의 row들과 old_p가 원소별 곱셉을 하고, 최종적으로 다 더하게 된다.
M을 transpose시키게 되면, 각 i 번째 row가 의미하는 것은 다음과 같다.
각 페이지에 대해 i번째 page로 가는 링크가 선택될 확률

[[0. 0.5 0. 0.5 0. ]
[0. 0. 0.5 0. 0. ]
[0.5 0.5 0. 0. 1. ]
[0. 0. 0.5 0. 0. ]
[0.5 0. 0. 0.5 0. ]]
위에서 구한 M의 경우, 위와같이 값이 나온다.
첫번째 row를 보면 v2, v4에서 v1으로 올 확률이 1/2이고 그래프를 다시 확인해보면, 맞다는 것을 알 수 있다.
최종적으로 우리가 예시에서 본 문제를 풀어보자.
1. 첫번째로 v1을 방문했을때, 두번째로 v3를 방문할 확률
[0.04 0.04 0.44 0.04 0.44]v3에 해당되는 값이 0.44이고 이는 11/25와 같다.
2. 첫번째로 v1을 방문했을때, 세번째로 v4를 방문할 확률
[0.072 0.216 0.424 0.216 0.072]v4에 해당되는 값이 0.216이고, 이는 27/125와 같다.
위 문제의 page rank는 벡터 p가 더이상 변화하지 않을때까지 반복해주면 된다.
import numpy as np
M = np.array([[0,0,1,0,1],
[1,0,1,0,0],
[0,1,0,1,0],
[1,0,0,0,1],
[0,0,1,0,0]], np.float32)
out_count = np.sum(M, axis=-1)[...,np.newaxis]
M = (M / out_count).T
p = np.array([1,0,0,0,0])
alpha = 4/5
eps = 1e-8
diff = 1
while diff >= eps:
old_p = p
p = (1-alpha)/5 + alpha*(M @ old_p)
diff = np.sum(np.abs(old_p - p))
print(p)[0.17342193, 0.16677741, 0.31694352, 0.16677741, 0.17607973]
Power method 방식으로 찾은 page rank는 위와 같다.
식을 통해 page rank를 찾기
손으로 power method를 계산한다고 하면, 위에서 사용했던 예시도 최소 35번 반복해야한다.
만약 시험지에 매 step마다 page별 방문 확률을 적어야한다고 하면, 손가락이 부러지는 불상사가 생길 수 있다.
이제부터는 수식을 세워서 page rank를 계산하는 방법을 사용해보자.

위 그래프에서 링크 방문 확률이 20%라고 했을때, page rank를 구해보자.
v4에 대한 방문 확률식을 구성하면 다음과 같다.

조금 계산해보면 알겠지만, v1~v3에 대한 방문 확률을 모두 동일하게 나온다.
따라서 t-1에 대한 방문확률을 k라는 변수로 합쳐서 다시 나타낼 수 있다.

이제 k에 대한 식을 세워보자.

Prob(v4, t)와 Prob(v4, t-1)은 t가 무한대로 갔을때 값이 같아지기 때문에 똑같이 변수 h로 놓고 식을 정리하면 다음과 같다.

위에서 구한 두 식에 대해 연립 방정식을 세워서 풀면 h와 k는 각각 1/3, 2/9가 나온다.
Power method 코드를 통해 구한 확률은 다음과 같다.
[0.22222222 0.22222222 0.22222222 0.33333333]
v1~v3에 대해 2/9, v4에 대해 1/3임을 알 수 있다.