이미지는 픽셀 단위로 이루어진 데이터이다.
픽셀 단위라는 것은 색깔을 가진 블록들을 하나하나 붙여서 만들었다는 것을 의미한다.
우리가 보는 휴대폰의 이미지나, 모니터의 이미지들 모두 픽셀로 이루어져 있으므로 자세히 들여다보면 무수한 정사각형들의 집합임을 알 수 있다.
하지만 현실의 물체들은 모두 연속적인 데이터이다. 픽셀처럼 딱 떨어지는 위치가 없다.
여기면 여기 저기면 저기, 어떤 기준점을 바탕으로 정확한 수치만큼 떨어져있다고 말하기 어렵다.
그림을 키워보자
생각해보자.
우리가 가진 고양이 사진이 있는데, 좀 크게 키워서 보고싶다.
고양이 사진은 높이가 640픽셀 너비가 480 픽셀이라고 하자.
우선 틀을 만들어야하므로 무작정 이미지의 높이를 2배하고 너비를 2배한 틀을 만들었다.
고양이 사진은 픽셀 단위로 이루어져 있다고 했는데, 우리가 가진 픽셀은 총 640 x 480개 밖에 없다.
즉 3 x 640 x 480 개나 부족하다!
이거 어디서 찾을까.

우선 아쉽긴하지만, 좀 적절히 배치해보자.
이 이미지는 500 x 500 픽셀로 이루어져있고, 이 이미지로 실험해보자.
import matplotlib.pyplot as plt
import numpy as np
image_height, image_width = image.shape[:2]
new_image = np.zeros((image_height*2, image_width*2, 3), np.uint8)
new_image_height, new_image_width = new_image.shape[:2]
for y in range(image_height):
for x in range(image_width):
new_image[y*2, x*2] = image[y, x]
plt.imshow(new_image)

높이와 너비를 보면 기존 이미지보다 커진것을 알 수 있지만, 아쉽게도 좀 어두워졌다.
색이 배치되지 않은 픽셀은 검정색이기 때문에 전체적으로 어두워보이는 것이다.
확대해서 보면 부족한게 더 잘 보인다.

저 사이사이 값들을 어떻게 채우면 좋을까?
영리한 친구는 픽셀과 픽셀 사이 평균값을 사용하면 되겠다고 할 수 있다.
한번 적용해보자.
mean_image = new_image.copy()
for y in range(new_image_height):
for x in range(new_image_width):
if new_image[y,x,0] == 0: # 픽셀이 검정색일때
try: # out of range 처리
# 양 옆 픽셀이 색이 존재한다면, 왼쪽 오른쪽 픽셀의 평균
if new_image[y,x+1,0] != 0:
for c in range(3):
mean_image[y,x,c] = int(new_image[y,x-1,c]/2 + new_image[y,x+1,c]/2)
# 양 옆 픽셀이 존재하지 않는다면, 위 아래 픽셀의 평균
else:
for c in range(3):
mean_image[y,x,c] = int(new_image[y-1,x,c]/2 + new_image[y+1,x,c]/2)
except Exception as e:
continue
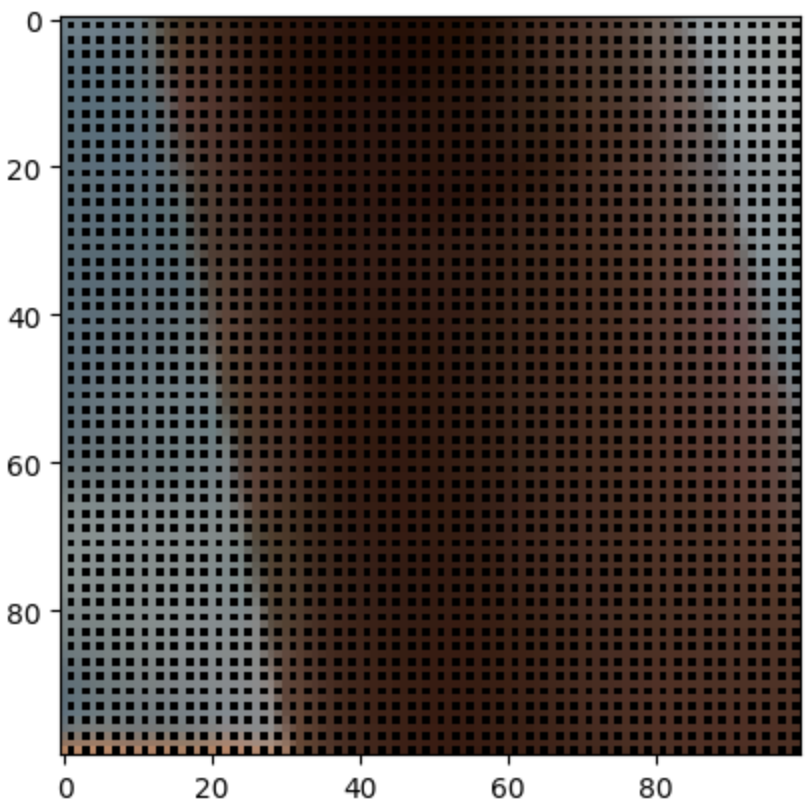
양 옆 혹은 위 아래에 픽셀들이 검정색이 아니라면, 두 픽셀의 평균을 넣었다.
이제 가운데 픽셀만 남았는데, 이 친구는 어떻게 할까?
위 코드를 살짝 수정해서 한번 더 돌리면 괜찮을것 같다.
#mean_image = new_image.copy()
for y in range(new_image_height):
for x in range(new_image_width):
if mean_image[y,x,0] == 0: # 픽셀이 검정색일때
try: # out of range 처리
# 양 옆 픽셀이 색이 존재한다면, 왼쪽 오른쪽 픽셀의 평균
if new_image[y,x+1,0] != 0:
for c in range(3):
mean_image[y,x,c] = int(mean_image[y,x-1,c]/2 + mean_image[y,x+1,c]/2)
# 양 옆 픽셀이 존재하지 않는다면, 위 아래 픽셀의 평균
else:
for c in range(3):
mean_image[y,x,c] = int(mean_image[y-1,x,c]/2 + mean_image[y+1,x,c]/2)
except Exception as e:
continue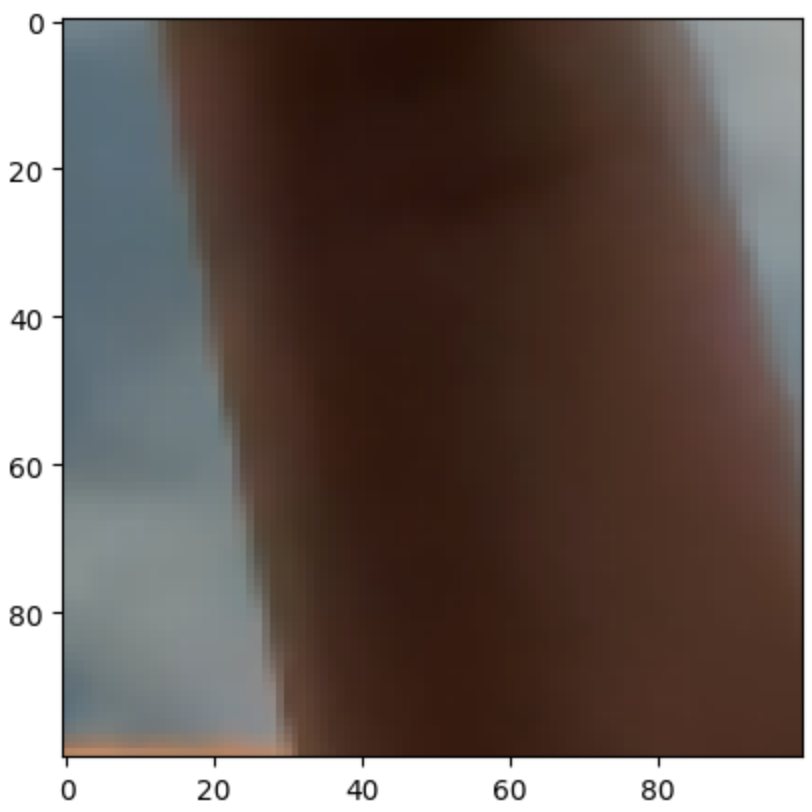
사실 위 코드는 완벽하지 않다.
티는 별로 안나지만 그림의 맨 끝에 해당하는 픽셀은 처리하지 않았다.
한계점
2배는 어찌저찌 양 옆 픽셀로 해결했지만, 3배, N배는 어떻게 해야할까?
색이 나올때까지 for문을 돌려야하나?
가운데가 더이상 비어있지 않을때까지 연속해서 코드를 돌려야 하기도 하고..
귀찮긴 하지만 구현하면 할 수 있을것 같긴 하다.
양 옆 혹은 위 아래 픽셀로부터 몇칸 떨어져 있는지에 따라 가중치를 주면서 평균을 주면 될것같다.
근데 코드가 굉장히 더럽고, 길어질 것 같다. 게다가 이게 최적의 효율임을 어떻게 보장하지?
알바 아니라면 상관없지만, 오늘의 주제인 Bilinear Interpolation 을 사용하면 훨씬 간단하게 처리가 가능하다.
Bilinear Interpolation
https://jonghank.github.io/ee212/final_projects/2019a/9/9.html
https://jonghank.github.io/ee212/final_projects/2019a/9/9.html
jonghank.github.io
위 블로그에서 맨 처음으로 나오는 이미지를 보면, 인형뽑기 기계가 어떻게 움직이는 지 대략적으로 유추가 가능하다.
먼저 왼쪽이나 오른쪽으로 조금 움직이고.. 그 다음 위 아래로 조금 움직여서 원하는 위치를 찾는다.
Bilinear interpolation은 정확히 이런 방식으로 보간(interpolation)을 수행한다.
Interpolation에 대한 설명은 나중에 하겠지만, 궁금한 사람은 직접 찾아보자.
간단히 말하면, 가지고 있는 데이터가 1초에 한번씩 0~5초까지 수집되었을 때, 0.5초 0.1 초에는 데이터가 어떻게 수집될지 예측하는 것이다.
즉, 여러개의 점을 지나는 함수를 찾는 것과 같다.
Bilinear interpolation은 인형뽑기와 같은 방식으로 값을 찾는다.
이미지에 대입하면, 4개의 픽셀이 가진 값을 통해 그 중간에 있는 색을 유추한다!
(0,0), (1,0), (0,1), (1,1) 픽셀 사이에 있는 (0.12837123, 0.84576626) 위치에 있는 색도 알 수 있다.
근데, 이걸 어떻게 써먹는다는 걸까?
도저히 위에서 했던 내용들과 이어지지가 않는다.
위의 코드의 흐름은 이렇다.
1. 원본의 (x, y)의 위치에 있는 픽셀 값을 크기를 키운 이미지의 (2x, 2y)위치에 넣는다.
2. 크기를 키운 이미지에 색을 넣는다.
2-1. 크기를 키운 이미지의 왼쪽과 오른쪽의 픽셀값이 검정색이 아니라면, 두 픽셀의 평균값을 넣는다.
2-2. 크기를 키운 이미지의 왼쪽과 오른쪽의 픽셀값이 검정색이라면, 위 아래 두 픽셀의 평균값을 넣는다.
3. 2번을 다시 한번 반복한다.
즉, 원본에서 시작해서 크기를 키운 이미지로 값을 옮기는 과정이라고 이해할 수 있다.
이제 반대로 생각해보자.
크기를 키운 이미지의 (x, y)위치에 있는 픽셀은 원본 이미지의 어느 위치의 픽셀을 의미할까?
당연히 (x/2, y/2)위치에 있는 픽셀일것이다.
하지만 2로 나눈 값이 정수라는 보장이 없다. 소수점을 무조건 포함한다.
예를들어 크기를 키운 이미지의 (1,1)에 있는 픽셀은 원본의 (0.5, 0.5)에 위치하는 픽셀이지만, 이 픽셀의 값을 알 수가 없다.
위 과정에서는 이를 해결하는 방법이 두 픽셀의 평균값이었다.
한계점에서도 인식했듯, 크기를 3배, 4배, 5.12배, 2.34 배를 한다고 하면 골치가 아파진다.
하지만 소수점에 해당하는 픽셀의 값을 알 수 있다면?
단 한 번의 3중 for문을 통해 크기를 키운 이미지를 완성시킬 수 있다.
이를 해결할 수 있는 방법이 바로 interpolation이고, 그중 Bilinear interpolation에 대해 알아보려한다.
수식에 대해
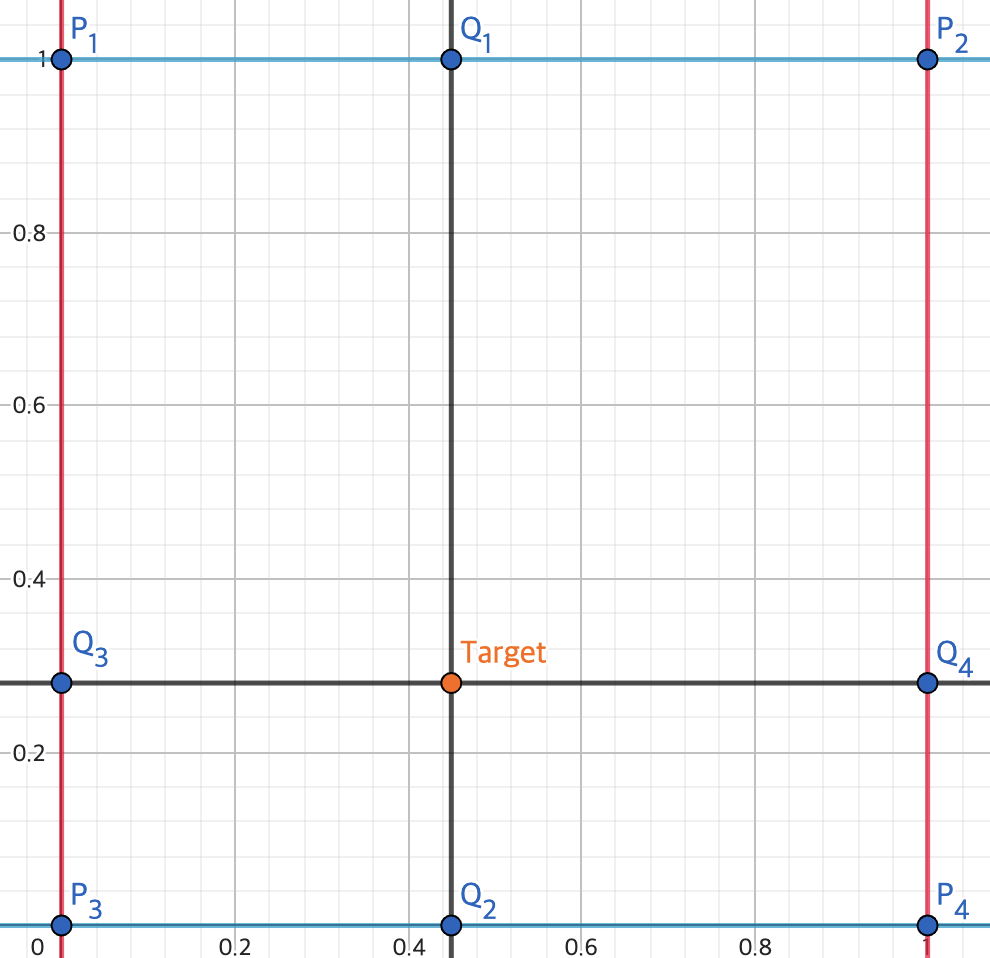
Target에 해당하는 점이 우리가 원하는 점이다.
Bilinear interpolation은 4개의 점을 필요로 한다. 특정 점을 기준으로 오른쪽, 아래, 대각선 하나씩 필요하다.
우선
즉,
특정 점의 픽셀 값을
3차원이기 때문에 위 그림은 점 4개를 위에서 내려다보고 있는 것으로 이해할 수 있다.
이제 y축을 지우고 x축과 픽셀값만 축으로 둬서 보면 다음과 같다.
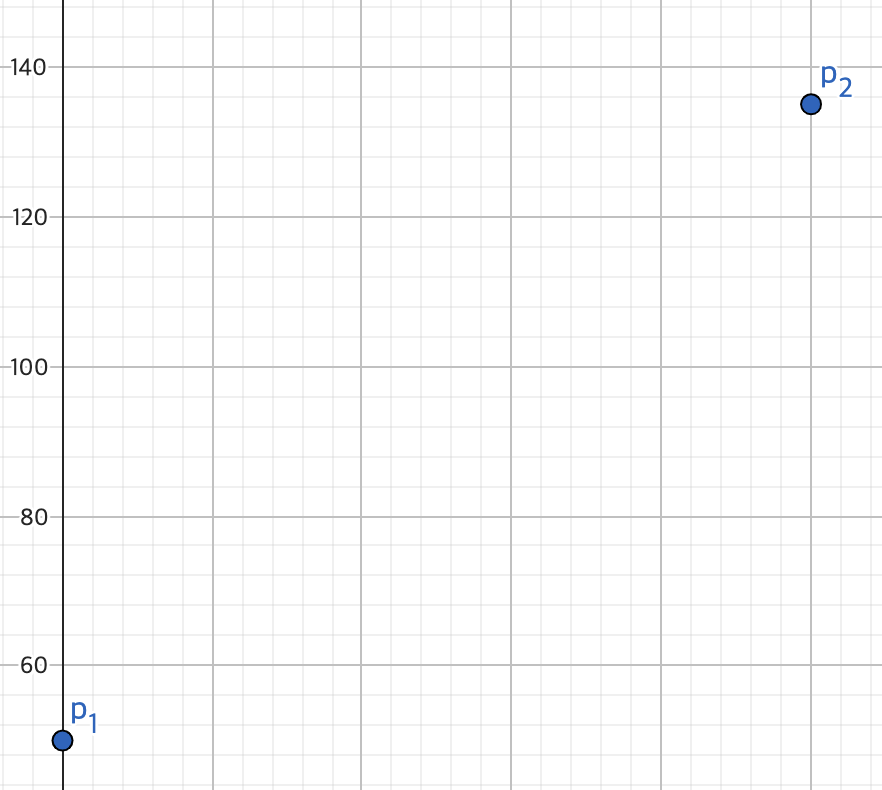
Bilinear 방식은 두 점(
따라서
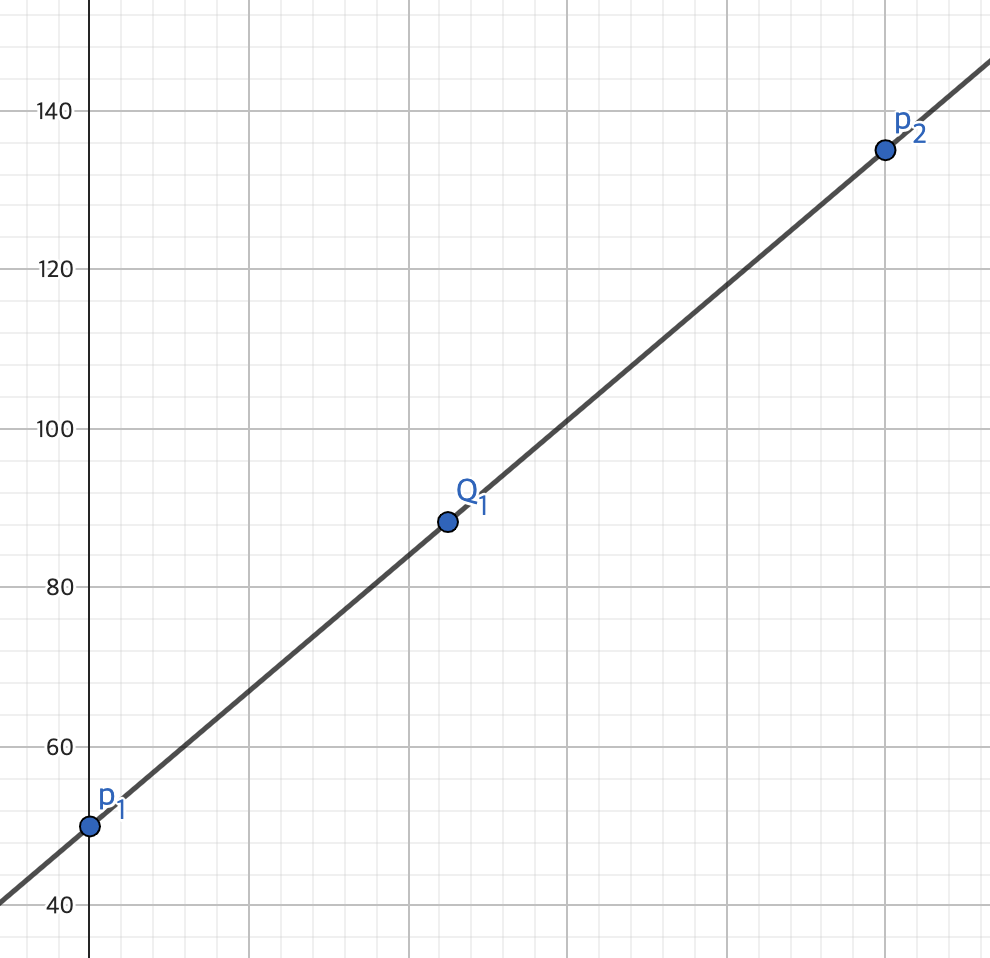
직선의 방정식을 일반화 하면 다음과 같다.
최종적으로

위 수식의 x위치에 Target(
Target에 해당하는 점은
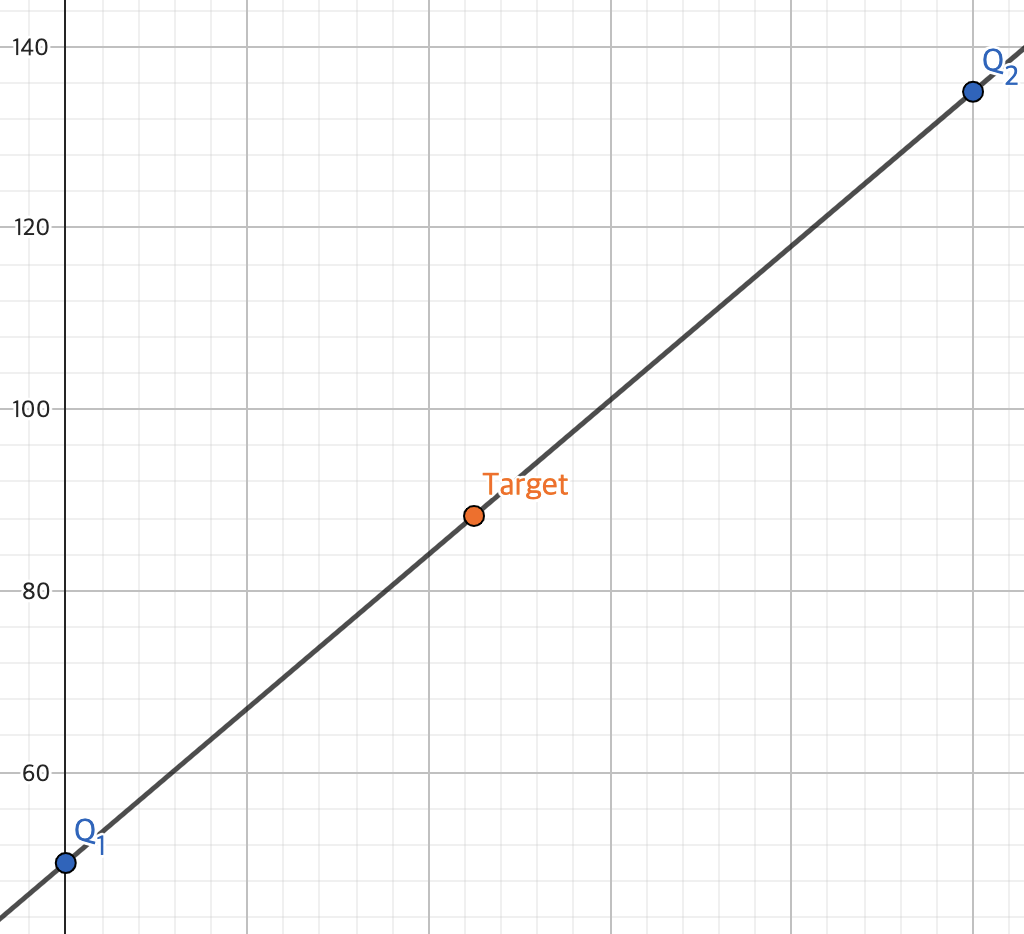
편의상
위 두 점은 y축과 픽셀값으로 구성됐음을 생각하고 식을 다시 구성하면 다음과 같다.
수식은 이제 징그러우니까 코드로 보자.
def bilinear_interpolation(points, tx, ty):
p1 = float(points[0][0])
p2 = float(points[0][1])
p3 = float(points[1][0])
p4 = float(points[1][1])
q1 = tx*p2 + (1-tx)*p1
q2 = tx*p4 + (1-tx)*p3
pixel_value = ty*q2 + (1-ty)*q1
return pixel_value코드도 더러울것 같았지만, 생각 이상으로 깨끗해졌다.
왜 이렇게 됐을까?
항상 인접한 오른쪽, 아래, 대각선에 위치한 픽셀을 가져오게되면, 상대적인 위치는 항상 1차이 밖에 나지 않는다.
굳이 절대적인 픽셀의 위치를 가져와서 더럽게 계산하는 것보다 훨씬 깔끔하게 계산 가능하다.
Bilinear Interpolation을 적용하여 크기를 마음대로 조절해보기
이번에는 0.8배를 해보자.
image_height, image_width = image.shape[:2]
scale_factor = 0.8
new_image = np.zeros(
(
int(image_height*scale_factor),
int(image_width*scale_factor),
3
), np.uint8)
new_image_height, new_image_width = new_image.shape[:2]
for y in range(new_image_height):
for x in range(new_image_width):
original_position_y = y/scale_factor
original_position_x = x/scale_factor
idx_y = int(original_position_y)
idx_x = int(original_position_x)
ty = original_position_y - idx_y
tx = original_position_x - idx_x
if 0<=idx_y+2<image_height and 0<=idx_x+2<image_width:
for c in range(3):
points = image[idx_y:idx_y+2, idx_x:idx_x+2,c]
new_image[y,x,c] = int(bilinear_interpolation(points, tx, ty))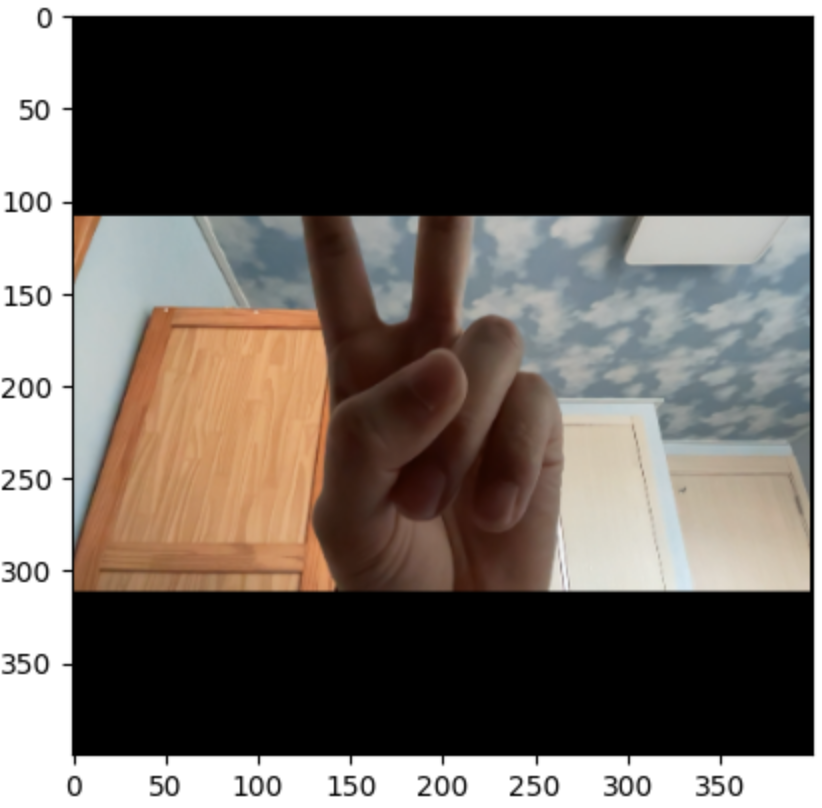
기존 이미지와 똑같이 보인다면 성공이다!
2배보다 크게 N배 할 수도 있으나, 꽤나 오랜 시간이 걸리기 때문에 꼭 해보고 싶다면 해보는 것을 추천한다.
2배를 하면 bilinear interpolation을 적용하기 전과 결과가 똑같이 나온다.
이유는 2배를 하는 과정에서 수행하는 계산들이 bilinear interpolation과 정확하게 일치하기 때문이다.
좀 더 빠른 방식
3개의 채널을 for문으로 돌리는 방식보다, 선형대수로 처리하는 방식이 조금 더 빠르기 때문에 코드를 적자면 다음과 같다.
import tensorflow as tf
import numpy as np
def scale_with_bilinear(image, scale_factor):
# 픽셀값들 정리
img_h, img_w = image.shape[:2]
left_top = tf.expand_dims(image[:img_h-1, :img_w-1], -2)
right_top = tf.expand_dims(image[:img_h-1,1:img_w], -2)
left_bottom = tf.expand_dims(image[1:img_h, :img_w-1], -2)
right_bottom = tf.expand_dims(image[1:img_h, 1:img_w], -2)
points_matrix = tf.cast(tf.concat([
left_top,
right_top,
left_bottom,
right_bottom
], axis=-2), tf.float64)
# resize 이전 좌표 얻기
new_h = int(scale_factor * img_h)
new_w = int(scale_factor * img_w)
grid = tf.meshgrid(tf.range(new_w), tf.range(new_h))
new_x = tf.cast(grid[0], tf.float64) / scale_factor
new_y = tf.cast(grid[1], tf.float64) / scale_factor
new_vec_x = new_x - tf.cast(tf.cast(new_x, tf.int32), tf.float64)
new_vec_y = new_y - tf.cast(tf.cast(new_y, tf.int32), tf.float64)
new_vec_x = tf.expand_dims(new_vec_x, -1)
new_vec_y = tf.expand_dims(new_vec_y, -1)
new_idx_x = tf.cast(new_x, tf.int32)
new_idx_y = tf.cast(new_y, tf.int32)
# 계수 정리
coef_left_top = (1-new_vec_x)*(1-new_vec_y)
coef_right_top = new_vec_x*(1-new_vec_y)
coef_left_bottom = (1-new_vec_x)*new_vec_y
coef_right_bottom = new_vec_x*new_vec_y
coef_matrix = tf.concat([
coef_left_top,
coef_right_top,
coef_left_bottom,
coef_right_bottom
], -1)
coef_matrix = tf.expand_dims(coef_matrix, -2)
# 이미지 생성
new_image = np.zeros((new_h, new_w, 3), np.uint8)
for y in range(new_h):
for x in range(new_w):
if 0 <= new_idx_y[y,x] < img_h-1 and 0 <= new_idx_x[y,x] < img_w-1 :
new_image[y,x] = coef_matrix[y,x] @ points_matrix[new_idx_y[y,x], new_idx_x[y,x]]
return new_image
결론
꽤 긴 내용이었지만, bilinear interpolation은 놀랍게도 이미지에 적용하는 interpolation에서 꽤나 빠른 방식이다.
그러나 결과물은 생각보다 많이 깨진다고 생각할 수 있고, 생각한게 맞다.
더 부드럽게 만들어주는 interpolation도 있고, 이는 포스팅을 이어가면서 차차 설명될 예정이다.
'컴퓨터 비전' 카테고리의 다른 글
| 3D keypoints 시각화 해보기 (0) | 2024.07.13 |
|---|---|
| Camera calibration (0) | 2024.07.06 |
| [컴퓨터 비전] Histogram Equalization (1) | 2023.03.21 |
| [컴퓨터 비전] 이미지 변환(1) (0) | 2022.02.04 |
