Analog & Digital
데이터는 그 형태가 연속적인지(continuous), 이산적인지(discrete)에 따라 각각 아날로그 데이터 그리고 디지털 데이터라고 부른다.
신호도 마찬가지로 아날로그 신호와 디지털 신호가 존재한다.


아날로그 신호는 모든 데이터들이 서로 굉장히 가깝게 붙어있기 때문에 어느 지점을 찍어도 그 지점에 대한 값을 알 수 있다.
그에 반해 디지털 신호는 아날로그 신호에 비하면 셀 수 있을만큼의 데이터들이 존재한다.
위의 그림에서 디지털 신호부분은 데이터를 일부러 파란 원으로 표시했다.
디지털 신호가 빨간 선으로 이어진건 그냥 보기 편하라고 저렇게 해놓은 것이지, 데이터들이 저렇게 분포해있지 않다.
Periodic & Nonperiodic
신호는 주기적(periodic)이거나 주기적이지 않다(nonperiodic).
주기적이라는 말은 신호가 패턴을 가지고 있다는 것을 의미한다.
그에 비해 주기적이지 않다라면, 패턴을 알 수가 없다는 것으로 이해할 수 있다.
주기적인 신호가 가지는 패턴은 일정한 주기(period)가 있다.
하나의 완벽한 패턴을 cycle이라고 부른다.
이런 주기나 패턴은 아날로그던 디지털이던 상관없이 나타날 수 있는 특징이다.
아날로그 신호가 주기적이면, 그 신호는 단일(simple)신호이거나, 합성(composite)신호이다.
단일 신호는 sine 파형(wave)이며, 더이상 분해할 수 없다.
반면 합성 신호는 여러개의 sine 파형으로 분해할 수 있다.
위에서 하나의 완벽한 패턴을 사이클이라고 한 이유는 sine 파를 쓰기 때문이다.
sine 함수는 x축으로 각도(0~360도, 0~2pi)를 사용한다.
따라서 한바퀴가 기준이 되고, 이걸 하나의 패턴으로 보는 것이다.
Analog Signal
아날로그 신호는 3가지 요소를 가진다.
1. 진폭(Amplitude)
2. 진동수(Frequency)
3. 위상(Phase) 또는 각도
이제 각각의 요소를 변화시키면, 사인파가 어떻게 변화할지 알아보자.
Amplitude에 따른 신호 형태
Amplitude는 진폭을 의미한다.
근데 진폭이 3이야~ 이렇게 말하지는 않는다.
진폭의 단위가 전압이기 때문이다.
그래서 진폭은 V(볼트)가 단위가 된다.
따라서 진폭이 몇V야~ 라고 하는 습관을 갖자.
진폭이 크다는 것은 상대적인 개념이라, 어떤 사인파(sine wave, 아날로그 신호)를 놓고 "이게 진폭이 큽니다." 이럴수가 없다.
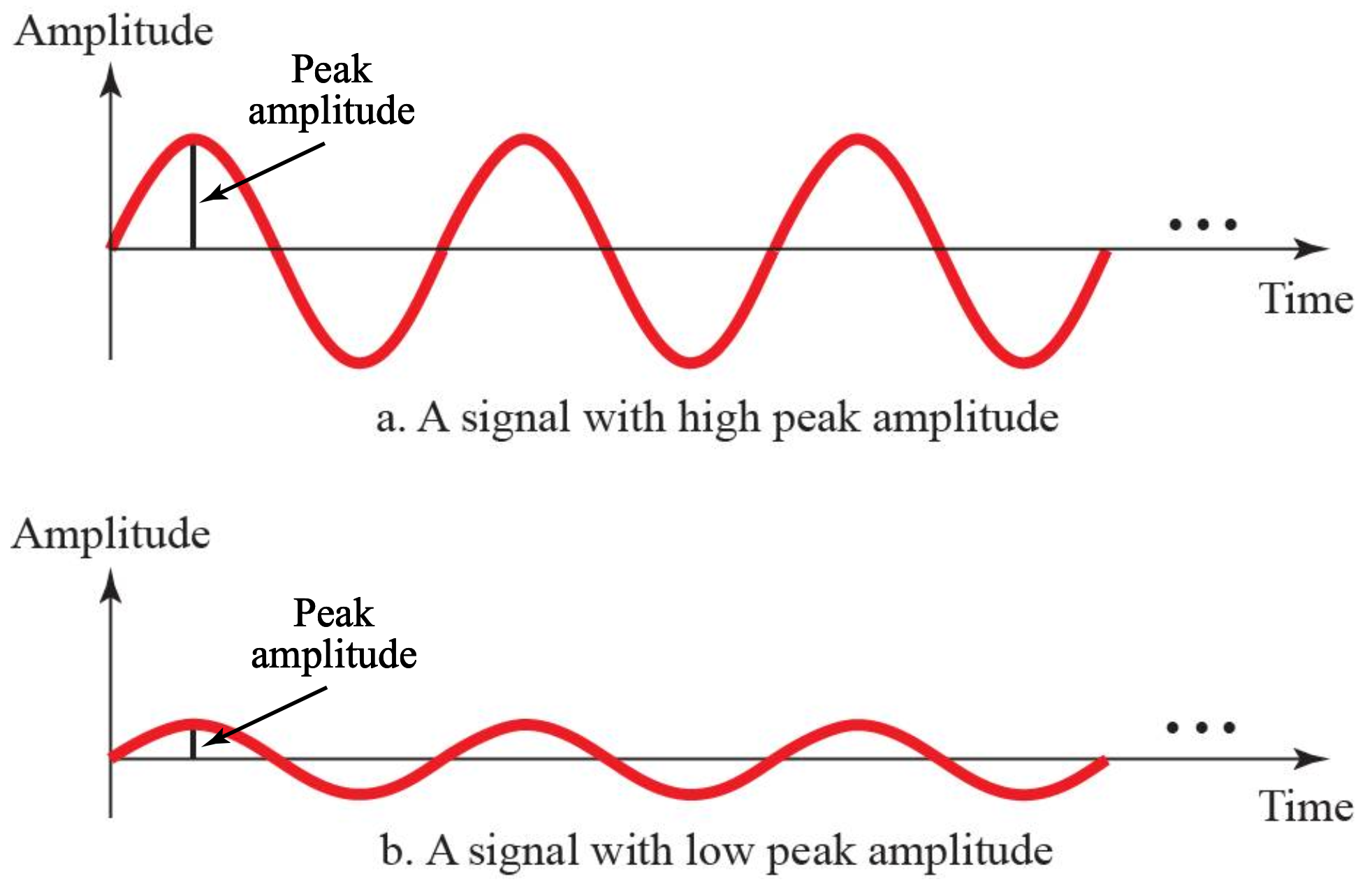
a와 b를 보면 진폭에 대해 감이 올것이다.
진폭이 커지면, 파동이 y축 방향으로 길어진다.
반면 작아지면 줄어든다.
따라서 a가 b보다 진폭이 크다고 할 수 있다.
위 사진에서 peak amplitude는 최대 진폭, 즉 사인파에서 전압이 가장 클때를 말한다.
Frequency에 따른 신호 형태
Frequency는 직역하면 빈도다.
무엇에 대한 빈도냐면, 1초에 사이클이 몇번 있는지를 말한다.
다른말로 하면, 진동수라고 한다.

위 신호는 주기(period)가 $1 \over 12$초인 사인파이다.
1초에 12번 사이클이 돈다는 말이다.
이 사이클의 빈도는 그대로 헤르츠(Hz)라는 단위를 사용할 수 있는데, 똑똑하게 말하고 싶으면 "위 신호는 12Hz네요~" 라고 하자.
주기와 진동수의 관계는 보다시피 역수다.
한 사이클을 도는데 주기가 0.5초면 진동수는 2Hz가 되는것이다.

주기가 $1 \over 6$초가 되면 진동수는 당연히 6Hz가 된다.
여기서 잠깐 진동수(frequency)에 대한 토막 상식을 알아보자.
위에서 이야기했던 패턴(사이클)은 변화가 없는 것도 패턴으로 생각할 수 있을까?
즉, 전압을 계속 1V만 준다거나, 0V만 준다거나 하면 이것도 하나의 패턴으로 생각할 수 있는가에 대한 고민이다.
당연히 주기가 굉장히 긴, 패턴으로 생각할 수 있다.
여기서 굉장히란 아예 무한으로 생각해도 무방하다.
진동수는 주기의 역수라고 했다.
주기가 미친듯이 길다면, 진동수는 미친듯이 작아진다.
따라서 우리가 정해놓은 시간동안 신호의 변화가 없었다면, 진동수는 0에 수렴하게 된다.
반면, 사이클의 주기가 굉장히 짧다면 어떨까?
주기가 짧으면 짧을수록 진동수는 커지기 때문에 진동수는 무한으로 발산한다.
Phase에 따른 신호 형태
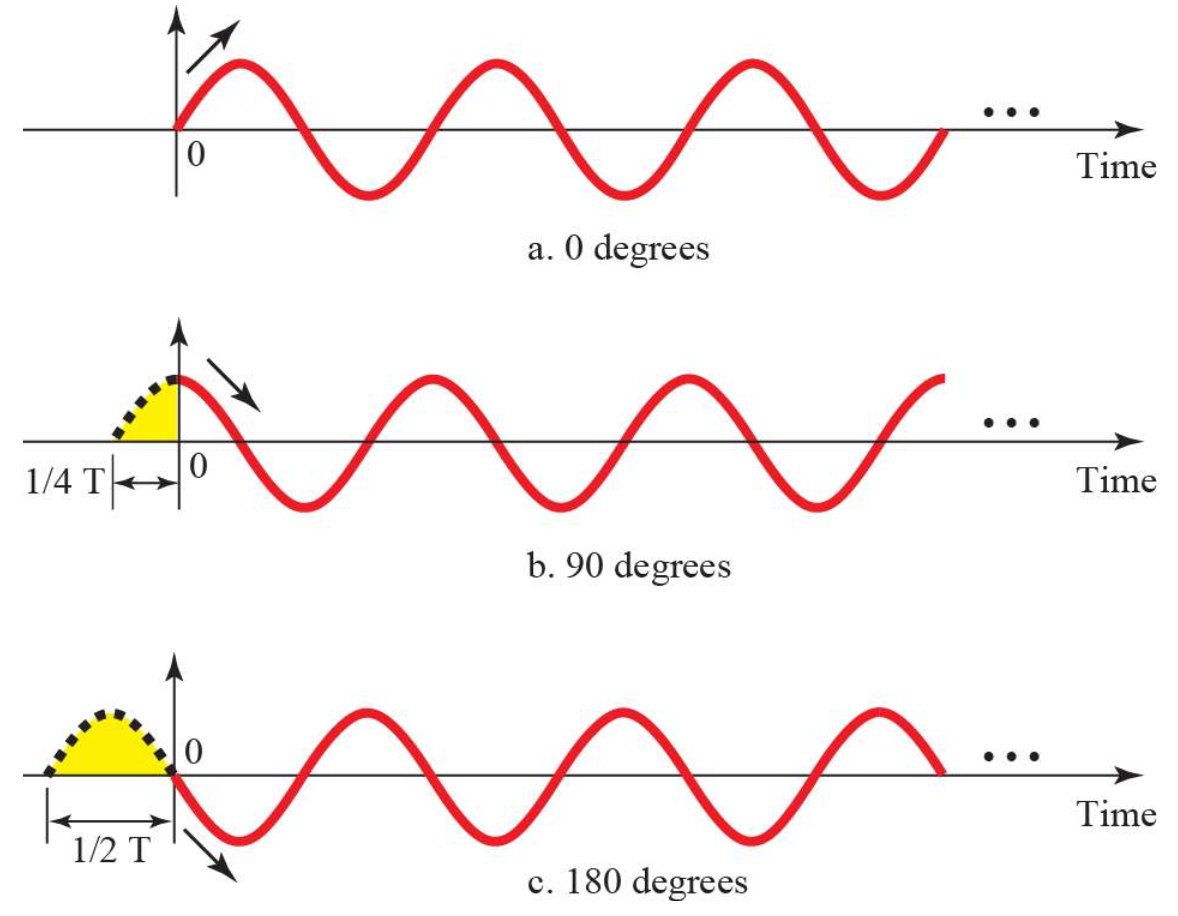
사인파는 x축이 각도와 대응된다.
즉, 각도에 따른 사인 함수의 함수값이 y축과 대응된다.
사인파로 보내는 신호의 요소중 위상(Phase)은 x축 방향으로의 대칭이동의 정도를 나타낸다.
말이 어렵기 때문에 식 하나로 설명하자면 다음과 같다.
$sin(x + phase)$
따라서 위상의 값(각도)이 0보다 커지면, 사인파가 왼쪽으로 이동되고
0보다 작아지면, 사인파가 오른쪽으로 이동한다.
Composite Signals
이제 합성 신호(composite signal)에 대해 알아보자.

합성 신호는 여러 단일 신호(simple sine wave)의 합으로 나타낼 수 있다.
위 그림처럼 디지털 신호와 단일 신호를 합성해서 진폭을 변화시킨다거나
다수의 단일 신호를 합해서 진동수를 변화시킬수도 있다.
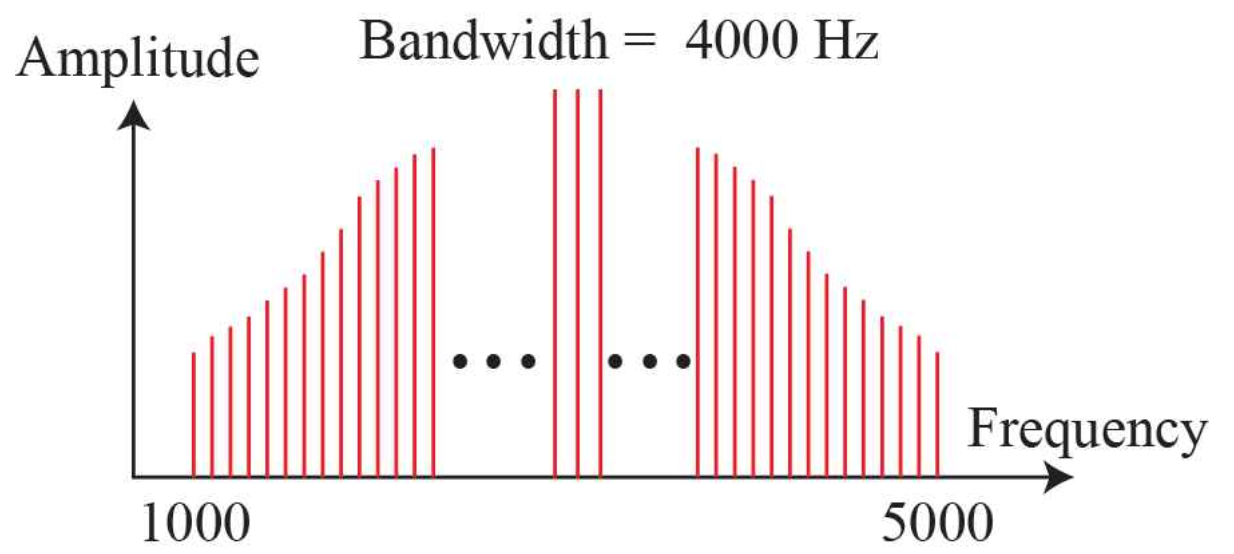
Bandwidth
대역폭(Bandwidth)은 신호의 최대 진동수와 최저 진동수를 빼서 구할 수 있다.
Digital Signals
지금까지 아날로그 신호만 봐서 섭섭했을 수 있는데, 그럴까봐 디지털 신호도 소개한다.
아날로그 신호는 사인파로 데이터를 전송했다면, 디지털 신호는 그런거 없이 그냥 전압으로 승부를 본다.
보내려는 디지털 데이터는 어차피 0이나 1로 이루어져있다.
만약에 신호 하나에 0 또는 1을 보낼 생각이라면(1 bit per 1 signal)
서로다른 전압을 2개 준비해야한다.
만약 신호 하나에 2bit를 보낼 생각이라면? 서로 다른 전압을 4개 준비해야한다.
즉, 신호 한번에 N개의 비트를 보낼지 정해졌다면 준비해야하는 전압은 $2^N$개다.

위 신호는 신호 한번에 1개의 비트(데이터)를 보내기때문에 전압(level)은 2개를 사용한다.
더불어 8개의 비트를 1초안에 보내는데, 이를 8 bit per second 라고 유식하게 말할 수 있다.
줄임말을 좋아한다면 8bps 라고해도 무방하다.
bps라는 단위를 갖는 이 값은 Bit rate 라고 부른다.
따라서 "위 신호는 bit rate이 8bps야~" 라고 말하면 된다.

위 신호는 신호 한번에 2개의 비트(데이터)를 보내므로 서로 다른 4개의 전압을 사용한다.
또한 1초에 16개의 비트를 보내므로 bit rate은 16bps 라고 말 할 수 있다.
Bit rate에 대해
디지털 신호는 이렇다 할 패턴이 거의 없다.
따라서 디지털 신호는 주기(period)라던지 진동수(frequency)라던지 하는 특징들을 들이대면 안된다.
대신에 디지털 신호는 bit rate(frequency를 대신한다.)이라는 특징을 가진다.
위에서 언급했듯, bit rate은 디지털 신호가 1초에 몇개의 비트를 보낼 수 있는지를 보이는 단위이다.
우리가 일상적으로보는 모니터를 생각해보자.
모니터의 높이와 너비가 1920 x 1080 이라고 가정하자.
한 픽셀은 4byte의 크기(RGBA)를 가진다.
따라서 우리가 가정한 모니터는 $1920 \cdot 1080 \cdot 4 \ byte = 1920 \cdot 1080 \cdot 32 \ bit$ 의 데이터를 표시한다고 할 수 있다.
모니터는 화면을 굉장히 빠르게 새로 고치는데, 이 빠르기를 헤르츠로 표시한다.
좋은 모니터면 아마 60Hz를 가질텐데, 1초에 60번 새로 표시한다는 말이된다.
그럼 위에서 가정한 모니터가 30Hz를 가진다고 하면, 1초에 몇개의 비트나 표시하는걸까?
위에서 구해봤듯 한 번 표시하기 위해 $1920 \cdot 1080 \cdot 32$ 비트를 사용한다.
이게 1초에 30번 깜빡이니까 여기에 30을 곱해주면된다.
따라서 1초에 약 1.9Gbps의 데이터를 받고, 보여준다고 할 수 있다.
디지털 신호는 아날로그 신호의 합성이다
위에서 디지털 신호에 대해 진동수(frequency)라는 특성을 들이대지 말자고 했다.
사실 들이댈수는 있는데, 좀 머리가 아파진다.
이 부분은 그냥 이해하지 않고 넘어가도 된다.
아날로그 신호를 설명할때, 합성 신호는 여러 사인파의 합으로 나타낸다고 했었다.
푸리에 변환이라는 걸 사용하면, 합성된 신호를 다시 여러 사인파의 합으로 분리할 수 있다.

위에서 이런 사진을 사용했었다.
잘 보면, 디지털 신호와 비슷한 파형을 여러 사인파의 합으로 나타냈다는 것을 알 수 있다.
근데 더 많은 사인파를 더하면, 거의 똑같이 만들어 낼 수가 있다.
주기가 있다면, 사인파로 분리해낼 수 있다.

주기가 있는 디지털 신호도, 무수히 많은 사인파의 합으로 나타낼 수 있다.
위 사진의 a를 보면, 주기가 명확하기 때문에 딱, 어떤 진동수를 갖는 사인파의 합인지로 분리할 수 있다.
근데 주기가 없는 b같은 디지털 신호는 어떻게 할까?
푸리에 변환은 신호 자체가 주기가 없다고 생각하고 나온 방법이 아니다.
주기가 없다라기 보단, 주기가 아주아주 긴 신호로 판단하고 분리를 시작한다.
따라서 저 신호를 만들기 위해 a보다 더 많은(거의 무한대에 가까운 개수의) 사인파의 합으로 나타나게 된다.
정확한 수식을 들이대고 설명을 길게 할 수 있지만, 이런 부분은 다른 블로그를 참고하는 것이 좋겠다.
'CS > 데이터 통신' 카테고리의 다른 글
| [데이터 통신] Multiplexing (0) | 2023.04.12 |
|---|---|
| [데이터 통신] Analog-to-Analog 변환에 대해 (1) | 2023.04.12 |
| [데이터 통신] Digital-to-Analog 변환에 대해 (0) | 2023.04.12 |
| [데이터 통신] Block coding과 Analog to Digital 변환 (3) | 2023.04.12 |
| [데이터 통신] Line coding에 대해 (4) | 2023.04.12 |